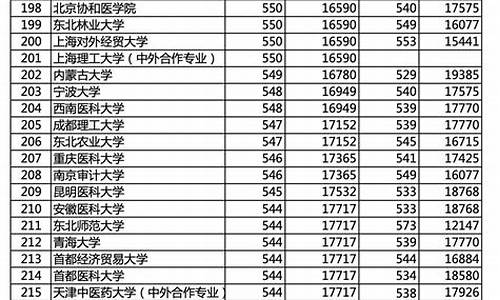
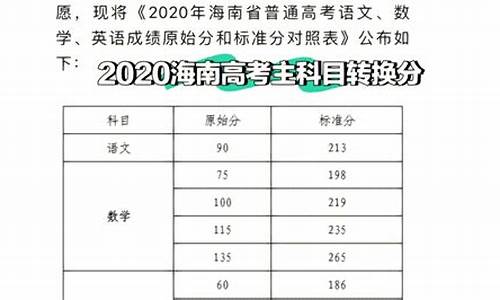
高考三角函数_高考三角函数公式大全表格

1.三角函数的应用在高考为什么很少考

2.高考对三角函数的要求

3.高考 三角函数题

4.一道高考三角函数探究题，求详细解答~~~~~~~~~~

1.w是正实数，函数f(x)=2sinwx在[-π/3,π/4]上是增函数，求w取值范围：

答案：0＜w≤3/2

sinx增区间（2kπ-π/2，2kπ+π/2）

sinwx增区间2kπ-π/2<wx<2kπ+π/2

区间包含0

所以应该在-π/2<wx<π/2

w>0

-π/2w<x<π/2w

（-π/3,π/4]是子区间

所以-π/2w<=-π/3

1/2w>=1/3

w<=3/2

π/4<=π/2w

w<=2

0<w<=3/2

答案：0＜w≤3/2

2.sin(π/2+a)+cos(π/2-a)=1/5a∈（0，π)求tana?

cos(a)+sin(a)=1/5

两边平方，

1+2sinacosa=1/25,

sin2a=-24/25,

cos2a=(1-sin^2(2a))^0.5=±7/25

cosa=±[(1±cos(2a))/2]^0.5

cosa=±4/5,cosa=±3/5

sina=±3/5sin=±4/5

a∈（0，π)

sina=3/5sina=4/5

cosa+sina=1/5

cosa=-3/5sina=4/5

tana=cosa/sina

答案：-4/3

3.函数y=sin(2x+π/6)-cos(2x+π/3)最小正周期和最大值？

y=sin(2x+π/6)-cos(2x+π/3)

=sin2x*(3^0.5/2)+cos2x*(1/2)-cos2x*(1/2)+sin2x*(3^0.5/2)

=3^0.5sin(2x)

最小正周期T=2π/2=π

最大值是√3

答案：π、1（想这种函数应该怎么处理？）

4、5π＜A＜6π，cosA/2=a,求sina/4?

sin(A/2)=±((1-cos(A/2)/2)^0.5

=±((1-a)/2)^0.5

5π＜A＜6π

5π/4＜A/4＜6π/4

sin(A/2)=-((1-a)/2)^0.5

-根号下1-a/2

5.∵根3sinx=-cosα

∴tanα=-根3/3

3^0.5sinα=-cosα

sinα/cosα=-3^0.5

tanα=sinα/cosα=-3^0.5

这两部是怎么回事啊，是怎么列出tanα这个式子的？

6.cos（α+β）=1/3,cos(α-β）=1/2，求log(5)tanαtanβ=？

sinsαinβ=-1/2[cos(α+β)-cos(α-β)]=-1/2(1/3-1/2)=1/12

cosαcosβ=1/2[cos(α+β)+cos(α-β)]=1/2(1/3+1/2)=5/12

log(5)tanαtanβ=log(5)(sinsαinβ/cosαcosβ)=log(5)(1/5)=-1

答案：1/6

7.已知f(x)=2sin(πx/4+π/4)，求f(1)+f(2)+f(3)+....+f(2011)?

f(1)=2sin(π/4+π/4)=2

f(2)=2sin(2π/4+π/4)=2^0.4

f(3)=2sin(3π/4+π/4)=0

f(4)=2sin(4π/4+π/4)=-2^0.4

f(5)=2sin(5π/4+π/4)=-2

f(6)=2sin(6π/4+π/4)=-2^0.4

f(7)=2sin(7π/4+π/4)=0

f(8)=2sin(8π/4+π/4)=2^0.4

f(9)=2sin(9π/4+π/4)=2sin(2π+π/4+π/4)=2sin(π/4+π/4)2

……

f(1)+f(2)+f(3)+....+f(8)=0

2011/8余3

f(1)+f(2)+f(3)+....+f(2011)=2+2^0.5

答案：2根下2+2

8.判断奇偶性：

f(x)=x?/sinx

g(x)=tanx+sinx

h(x)=lg(sinx+跟下（1+sin?x）)

f(-x)=(-x)^2/sin(-x)=-x?/sinx=-f(x)

g(-x)=tan(-x)+sin(-x)=-(tanx+sinx)=-g(x)

h(-x)=lg(sin(-x)+(1+sin?(-x)^0.5)=lg(-sinx+(1+sin?x)^0.5)=-h(x)

都是奇函数

答案：都是奇函数

9.扇形周长6，面积是2，求扇形中心角的弧度数？

A*r=6A=6/r

3.14r^2=2r=(2/3.14)^0.5

A=6(2/3.14)^0.5

答案：1或4

附加题：“根号下”怎么打符号？

^0.5

三角函数的应用在高考为什么很少考

解：f(x)=√3sinwx+coswx=2sin（wx+π/6）

∵该函数图像与直线y=2的两个相邻交点的距离等于π

∴该函数周期T=π=2π/w

∴w=2

∴f（x）=2sin（2x+π/6）

令-π/2+2kπ≤2x+π/6≤π/2+2kπ

k∈Z

得：kπ-π/3≤2x+π/6≤kπ+π/6

k∈Z

答案应该为C

高考对三角函数的要求

不少考。根据查询高三网可知，三角函数的应用在高考是重点内容，所以三角函数的应用在高考没有很少考。三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

高考 三角函数题

高考数学三角函数知识中的难点较多，很多学生都难以理解深刻。下面学习啦小编给大家带来高考数学三角函数重点考点，希望对你有帮助。

高考数学三角函数重点考点(一)

由解析式研究函数的性质

常见的考点：

求函数的最小正周期，求函数在某区间上的最值，求函数的单调区间，判定函数的奇偶性，求对称中心，对称轴方程，以及所给函数与y=sinx的图像之间的变换关系等等。

对于这些问题，一般要利用三角恒变换公式将函数解析式化为y=Asin(ωx+φ)的形式，然后再求相应的结果即可。

在这一过程中，一般要先利用诱导公式、二倍角公式、两角和与差的恒等式等将函数化为asinωx+bcosωx形式(其中常见的是两个系数a、b的比为1：1，1:1)，然后再利用辅助角公式，化为y=Asin(ωx+φ)即可。

高考数学三角函数重点考点

高考数学三角函数重点考点(二)

根据条件确定函数解析式

这一类题目经常会给出函数的图像，求函数解析式y=Asin(ωx+φ)+B。

A=(最大值-最小值)/2;

B=(最大值+最小值)/2;

通过观察得到函数的周期T(主要是通过最大值点、最小值点、“平衡点”的横坐标之间的距离来确定)，然后利用周期公式T=2π/ω来求得ω;

利用特殊点(例如最高点，最低点，与x轴的交点，图像上特别标明坐标的点等)求出某一φ';

最后利用诱导公式化为符合要求的解析式。

高考数学三角函数重点考点

高考数学重点考点

考点一：集合与简易逻辑

集合部分一般以选择题出现，属容易题。重点考查集合间关系的理解和认识。近年的试题加强了对集合计算化简能力的考查，并向无限集发展，考查抽象思维能力。在解决这些问题时，要注意利用几何的直观性，并注重集合表示方法的转换与化简。简易逻辑考查有两种形式：一是在选择题和填空题中直接考查命题及其关系、逻辑联结词、 “充要关系”、命题真伪的判断、全称命题和特称命题的否定等,二是在解答题中深层次考查常用逻辑用语表达数学解题过程和逻辑推理。

考点二：函数与导数

函数是高考的重点内容，以选择题和填空题的为载体针对性考查函数的定义域与值域、函数的性质、函数与方程、基本初等函数(一次和二次函数、指数、对数 、幂函数)的应用等，分值约为10分，解答题与导数交汇在一起考查函数的

一道高考三角函数探究题，求详细解答~~~~~~~~~~

第3题这种类型的题的解法是：

把sinxcosx化成sinx+cosx的形式，然后设sinx+cosx=t，再根据t的范围求解函数的最值，如下：

设t=sinx+cosx

那么t=sinx+cosx

=√2[(√2/2)sinx+(√2/2)cosx]

=√2[cos(π/4)sinx+sin(π/4)cosx]

=√2sin(x+π/4)

∴t∈[-√2，√2]

又∵t?=(sinx+cosx)?

=sin?x+2sinxcosx+cos?x

=1+2sinxcosx

∴sinxcosx=(t?-1)/2

∴y=[(t?-1)/2]+t，t∈[-√2，√2]

抛物线y的对称轴是t=-1

∴t=-1时y(min)=-1；t=√2时y(max)=(√2)+1/2

或者化成完全平方加一个常数的形式：y=(1/2)(t+1)?-1来计算也很容易。

括号打的有点多，怕你误解，相信以你的水平也不会，肯定能看懂的是吧！

总之，对于三角函数的计算要把公式与公式的转化运用的非常熟练，另外做过的题一定要看到题就想到思路，不要过一段时间再回来做就忘的差不多了那样的，到高考会很纠结的。

还有一种解法是求导，不知你们现在高中学了没，反正我们那时候好像没学过积的导数，三角函数的导数公式忘了学过没。。。(sinx)＇=cosx；(cosx)＇=-sinx

方法如下：(积的导数公式：(uv)＇=u＇×v+u×v＇，其中u，v都是x的函数)

y＇=(sinx)＇cosx+sinx(cosx)＇+(sinx)＇+(cosx)＇

=cos?x-sin?x+cosx-sinx

=(cosx-sinx)(cosx+sinx+1)

=√2cos(x+π/4)[√2sin(x+π/4)+1]

令y＇=0，得cos(x+π/4)=0或√2sin(x+π/4)+1=0

得x+π/4=(2m+1)π或x=(2k-1/2)π±π/4

再代入求最值，当然这个比较麻烦点，在某些场合用导数会更简便。

对于三角函数，不到万不得已不要用万能公式，另外你们应该也做过用万能公式的题，也就那些题型记住就行了，其他的看着办。

第5题，看来你基础知识没学好，把高一第一册课本的奇偶函数那一节翻出来看是怎么定义的！

奇函数可以这么理解：定义域关于原点对称，函数图象关于原点对称，对于三角函数来说，在定义域关于原点对称的基础上，只要函数过原点，也就是把点(0，0)代入可以使方程成立那么就是奇函数。

相应地，偶函数是定义域关于原点对称，函数图象关于y轴对称的函数。对于三角函数来说，定义域关于原点对称的基础上，x=0是函数的一个极值点就是偶函数，也就是在图象上x=0的点是最高点或者最低点，或者在x=0处的导数等于0，都是可以用来判定的。

你这个例子，你们老师说把它当整体看，是说括号内整体等于t，那么t=0时cosx取最大值，但是此时x=-9π/4≠0，也就是说x和t不是同一个概念，x=-9π/4才是f(x)的对称轴。反过来看，当x=0时t=9π/2，f(0)=0，也就是过原点，是奇函数。

你所认为的cosx是偶函数，是标准的余弦函数，也就是不平移，不伸缩，但是f(x)是在cosx的基础上平移和伸缩了的，当你把cosx向右平移π/2时就变成了sinx的标准情况，也就是y=cos(x-π/2)是奇函数，所以不能笼统的说以cos开头的函数就是偶函数，还是得求对称轴的。

其他的题应该是比较简单的，我有时间再算，挺忙的。有不懂的再留言！

希望能给你带来帮助。

已知函数f（x）=bsinwx（b∈R），x∈R，且图象关于点（π/3,0）对称，在x=π/6处f（x）取得最小值，求符合条件的w的集合

解析：∵函数f（x）=bsinwx（b∈R），x∈R

∵f（x）图象关于点（π/3,0）对称，满足f(x)+f(2π/3-x)=0

又∵f（x）图象在x=π/6处取得最小值，图像关于直线x=π/6对称，满足f(x)-f(π/3-x)=0

一般地，函数y=f(x)图像既关于点A(a,c)成中心对称又关于直线x=b成轴对称（a≠b），则y=f(x)是周期函数，且4|a-b|是其一个周期。

∴f（x）图象周期为T=4|π/3-π/6|=2π/3

∴w=2π/(2π/3)=3

∴f（x）=bsin3x==>f（π/6）=bsinπ/2=-b==>b=-1

∴f（x）=-sin3x

令f（π/3）=sin(wπ/3)=0

wπ/3=2kπ+π==>w=6k+3 (由负变0)

令f（π/6）=sin(wπ/6)=-1

wπ/6=2kπ-π/2==>w=12k-3

取二者最小公倍数w=3(2k+1)(4k-1)=24k^2+6k-3

取w={w|w=(-1)^k*(24k^2+6k-3),k∈N}

验证：

K=0时，f(x)=sin(-3x)==> f(π/6)=sin(-3π/6)=-1, f(π/3)=sin(-3π/3)=0

K=1时，f(x)=sin(-27x)==> f(π/6)=sin(-27π/6)=-1, f(π/3)=sin(-27π/3)=0

K=2时，f(x)=sin(105x)==> f(π/6)=sin(105π/6)=-1, f(π/3)=sin(105π/3)=0

……