1.高考常考的空间几何体

高考空间几何大题不用建模_高考空间几何大题

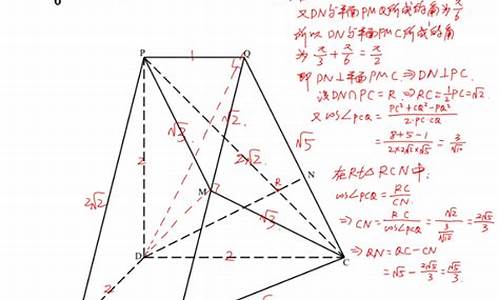
1：过M作AB的垂线MD，并连接CD、SD。则有MD//=1/2AP。=》MD垂直于面ABC，=》MD的垂直于SN。而AC=1/2AB=》 AD=AB 。所以<ADB=45。又有SD=1/2AB、ND=NA=1/2AB。所以<DNS=45。（能推出NS的长度为二分之根号二，第二问用到。）所以就有CD垂直于NS。所以NS垂直于面CDM，所以CM垂直于SN。

2：根据：V(M-CNS)=V(S-CMN)可以求求得点S到平面CMN的距离，而由第一问中得出的NS的长度。即可用三角函数把角表示出来。

高考常考的空间几何体

文科数学高考立体几何大题不能用空间向量解，那道题主要就是考察空间向量的。

数学上，立体几何(Solid geometry)是3维欧氏空间的几何的传统名称—- 因为实际上这大致上就是我们生活的空间。一般作为平面几何的后续课程。立体测绘(Stereometry)处理不同形体的体积的测量问题：圆柱，圆锥， 锥台，?球，棱柱，?楔，?瓶盖等等。?毕达哥拉斯学派就处理过球和正多面体，但是棱锥，棱柱，圆锥和圆柱在柏拉图学派着手处理之前人们所知甚少。

尤得塞斯(Eudoxus)建立了它们的测量法，证明锥是等底等高的柱体积的三分之一，可能也是第一个证明球体积和其半径的立方成正比的。

空间几何的出题类型

1.给出一个已知形状的几何体，用棱长关系或角度关系求某些棱长或夹角或某些面的面积或某些部分的体积

2.条件相似，证明某些棱、角相等、成比例或某些棱、面之间平行、垂直（即成角90°）或某些三角形相似、全等

3.条件相似，给出一个或几个动点，求某些边之间的函数关系

4.条件相似，求点或棱到特定的棱或面的距离

5.条件相似，问题全部换成向量的关系（如向量平行、法向量、法平面等）