2015高考江苏卷物理_2015江苏高考物理压轴题

1.2015年江苏高考时间安排，具体到每科的时间

2.高考。江苏。物理。

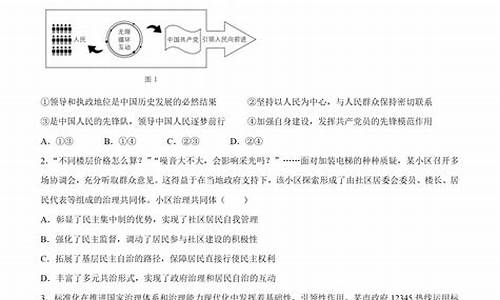
2023年江苏高考物理难度适中。

1、江苏高考物理试卷难度分析。

江苏高考物理试卷总体来说不难，江苏高考物理试卷在保持“新颖、灵活、扎实”的风格基础上，进一步凸现了必备知识、关键能力、学科素养、思维方法和创新意识的考查。

2、试题难度与历年数据对比。

从2016年到2021年的江苏高考物理试题难度系数分别为1.22、1.22、1.23、1.20、1.18和1.20。这几年的试题难度整体上呈现稳定的状态，波动不大。从历年数据来看，2023年江苏高考物理试题的难度可能也会保持在这个范围内。

3、试题命题方向和趋势。

从历年试题来看，江苏高考物理试题的命题方向比较全面，覆盖了力学、电学、光学、热学、原子物理等多个领域。试题也注重考查学生的实验能力和物理概念的理解。

如何备考物理科目：

1、熟悉考纲和重点。

仔细阅读并熟悉高考物理科目的考纲，了解考试要求和重点内容。重点关注重要的知识点、公式和实验原理，确保对考试内容有全面的了解。

2、整理知识框架。

物理是一个系统性的学科，建立一个清晰的知识框架对于理解和掌握各个概念和关系非常重要。整理笔记、制作思维导图或复习笔记，帮助你整合和记忆知识，准确把握各个知识点之间的联系。

3、多做例题和习题。

通过做大量的例题和习题，加深对知识点的理解，提高解题能力。重点练习一些常考的题型，例如力学题、电路题、光学题等。同时，注重分析解题思路和方法，培养解决问题的能力。

以上数据来自于高考助手网官网。

2015年江苏高考时间安排，具体到每科的时间

理科高考总分各省不尽相同，2015年绝大多数省份使用全国卷，总分为750分，但还有部分省市使用地方卷，计分方式不尽相同；比如，?江苏省总分为480分，上海市总分660，而浙江省总分为750分，但考试方式与全国卷不一样。具体规定如下。

普通高等学校招生全国统一考试（The National College Entrance Examination ）简称高考，是中华人民共和国（不包括香港、澳门、台湾）合格的高中毕业生和具有同等学力的考生参加的选拔性考试。

一、全国卷“3+X”

应用地区：大部分省市区

“3”指“语文、数学、外语”，“X”指由指学生根据自己的意愿，自主从文科综合（涵盖政治、历史、地理）和理科综合（涵盖物理、化学、生物）2个综合科中选择一个考试科目。此方案是目前全国应用最广，最成熟的，最被人们接受的。总分750分（语文150分，数学150分，外语150分，文科综合/理科综合300分）。

二、江苏卷“3+学业水平测试+综合素质评价”

应用地区：江苏

经过教育部批准，从2008年起，江苏省实行“3+学业水平测试+综合素质评价”高考方案。其中，“3”指“语文、数学、外语”，语文160分（文科加考40分加试题）、数学160分（理科加考40分加试题）、外语120分，满分480分。学业水平测试必修科目考试含物理，化学，生物，政治，历史，地理，信息技术7科，各科原始满分为100分，考生需参加未选为学业水平测试选修科目的5门必修科目。学业水平测试选修科目考试含物理，化学，生物，政治，历史，地理6科，各科原始满分120分，文科考生必考历史，理科考生必考物理，再从化学，生物，政治，地理中选一门，普通类考生须全部达C等方可参加高考和选修科目测试。学业水平测试实行等级计分，分为4个：A、B、C、D。（此方案由于总分偏低，且选修科目不计入总分，造成分数段扁平密集，另外物理，化学科目不计入总分，造成理科人才选拔困难，因此该方案很受争议）。

三、上海卷“3+3”

必考科目：语文/数学/英语每科150分 其中英语一年两考，取最高分。物理，化学，生物，政治，历史，地理选3门，每科70分，按照A A+……比例给分。其中地理等级考在高二，2017年加试地理考试将于2016年5月7日参加地理等级考。总分660分。

四、浙江卷“3+3”

必考学科：语文150分，数学150分，外语150分。选考学科：政治、历史、地理、物理、化学、生物、技术，学生要选择3门作为高考选考科目。选考科目每年会安排2次考试，分别在4月和10月进行。每门总共安排3次统一考试，考生可自行决定参加时间，每门科目最多参加2次，选考科目成绩实行等级赋分，如成绩在前1%者赋分100分加入高考总成绩。总分750分。

高考。江苏。物理。

2015年江苏省高考将于6月7日至8日进行，具体考试时间如下：

时间

科目

6月7日

9:00—11:30

语文(文科考生考试时间另增加30分钟)

15:00-17:00

数学(理科考生考试时间另增加30分钟)

6月8日

15:00-17:00

英语

6月9日

9:00—10:40

物理、历史

15:00—16:40

化学、生物、政治、地理

外语考试科目分英语、日语、俄语、德语、法语、西班牙语等6个语种，由考生任选其中一种参加考试。

报考外语专业的考生，须参加省中小学[微博]教研室组织的英语口语测试或省教育考试院组织的非英语语种外语口语测试，且成绩较好。

报考体育类、艺术类专业的考生，除必须参加全国文化统考和七门科目学业水平测试外，还须按有关规定参加省教育考试院、招生高校组织的专业考试。

弹簧类问题专题复习

弹簧类问题含有力的非突变模型---弹簧模型，这类问题能很好地考查同学们对物理过程的分析、物理知识的综合、以及数学知识的灵活应运，所以这类问题在近年的高考中频频出现。为了帮助同学们复习好这部分内容，现浅谈如下几点，供同学们参考

一、知识点聚焦

1、 弹簧的瞬时问题

弹簧发生弹性形变时，弹力与其形变量成正比，因此，弹力不同，形变量不同，形变量不同，对应的弹力也不同。解决这一类问题时一定要弄清“时刻”及“位置”的含义。

2、弹簧的平衡问题

这类问题涉及的知识有胡克定律、力的平衡条件，一般可用f=kx或△f=k?△x和∑F=0等公式来求解。

3、弹簧的非平衡问题

这类问题主要是指弹簧在相对位置发生变化时，所引起的力、加速度、速度、功、能和合外力等其他物理量发生变化的情况。这类问题的解决，不但要涉及胡克定律、牛顿第二定律、还要涉及动能定理、能的转化和守恒定律等方面的内容。

4、 弹簧弹力做功与动量、能量的综合问题

在弹簧弹力做功的过程中弹力是个变力，所以这类问题一般与动量、能量联系，以综合题的形式出现。这类问题有机地将动量守恒、机械能守恒、功能关系和能量转化等结合在一起，考查同学们的综合应用能力。解决这类问题时，要细致分析弹簧的动态过程，综合利用动能定理和功能关系等知识解题。

二、典型例题分析

例1．如图1所示，劲度系数为 K的轻质弹簧一端与墙固定，另一端与倾角为θ的斜面体小车连接，小车置于光滑水平面上。在小车上叠放一个物体，已知小车质量为 M，物体质量为m，小车位于O点时，整个系统处于平衡状态。现将小车从O点拉到B点，令OB=b，无初速释放后，小车即在水平面B、C间来回运动，而物体和小车之间始终没有相对运动。求：(1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小；(2)b的大小必须满足什么条件，才能使小车和物体一起运动过程中，在某一位置时，物体和小车之间的摩擦力为零。

解析；(1)所求的加速度a和摩擦力f是小车在B点时的瞬时值。取M、m和弹簧组成的系统为研究对象，由牛顿第二定律：kb=(M+m)a 所以a=kb/(M+m)。

　 取m为研究对象，在沿斜面方向有：f-mgsinθ=macosθ

所以， =

(2)当物体和小车之间的摩擦力的零时，小车的加速度变为a’，小车距O点距离为b’，取m为研究对象，有：mgsinθ=ma’cosθ

取M、m和弹簧组成的系统为研究对象，有 kb‘=(M+m)a’

以上述两式联立解得：b’=

　 点评：在求解加速度时用整体法，在分析求解m受到的摩擦力时用隔离法。整体法和隔离法两者交互运用是解题中常用的方法，希读者认真掌握。

例2.将金属块m用压缩的轻弹簧卡在一个矩形箱中，如图2所示，在箱的上顶板和下底板装有压力传感器，箱可以沿竖直轨道运动.当箱以a=2.0 m/s2的加速度竖直向上做匀减速运动时，上顶板的传感器显示的压力为6.0 N，下底板的传感器显示的压力为10.0 N.（取g=10 m/s2）

求：（1）金属块m的质量是多大;?

（2）若上顶板传感器的示数是下底板传感器的示数的一半，则箱子的加速度是多大.?

解析: 上顶板压力传感器显示的压力是金属块对上顶板的压力，大小也等于上顶板对金属块向下的压力；下底板传感器显示的压力为弹簧对下底板的压力，大小也等于弹簧对金属块向上的压力.根据金属块的受力情况和牛顿第二定律，即可求出质量、加速度.

（1）设上顶板的传感器显示的压力为FN1，下底板的传感器显示的压力为FN2，

由牛顿第二定律： mg+FN1-FN2=ma?

解得：m=0.5 kg

（2）由于弹簧长度不变，则下底板的传感器显示的压力仍为10.0 N，

即 FN2′=FN2=10 N?则上顶板的传感器显示的压力为FN1′=5 N

由牛顿第二定律： mg+FN1′-FN2′=ma′

解得： a′=0

例3.如图3所示，两个木块质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上（但不拴接），整个系统处于平衡状态，现缓慢向上提上面的木块，直到它刚离开上面的弹簧，在这过程中下面木块移动的距离为( )

解析：此题用整体法求最简单。由题意可将m1、m2视为一系统（整体），整个系统处于平衡状态，即∑F=0

故F=(m1+m2)g

由胡克定律知 F=k2x总

解得 x=

此x为系统下移的总距离，当缓慢向上提上面木块m1，直到它刚离开上面弹簧时，有 x’‘=，由题意可知，在这过程中下面木块移动的距离为 Δx=x－x’=

故本题选C.

点评：尽管此题初看起来较复杂，但只需选用整体法来分析求解，问题就会迎刃而解。

例4.在原子物理中，研究核子与核子关联的最有效途经是“双电荷交换反应”。这类反应的前半部分过程和下面力学模型类似。两个小球A和B用轻质弹簧相连，在光滑的水平直轨道上处于静止状态。在它们左边有一垂直轨道的固定档板P，右边有一小球C沿轨道以速度v0射向B球，如图7所示，C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变。然后，A球与档板P发生碰撞，碰后A、D静止不动，A与P接触而不粘连。过一段时间，突然解除锁定（锁定及解除锁定均无机械能损失），已知A、B、C三球的质量均为m。

（1）求弹簧长度刚被锁定后A球的速度。

（2）求在A球离开档板P之后的运动过程中，弹簧的最大弹性势能。

解析：整个过程可分为四个阶段来处理．

（1）设C球与B球粘结成D时，D的速度为v1，由动量守恒定律，得

mv0＝2mv1，　①

当弹簧压至最短时，D与A的速度相等，设此速度为v2，由动量守恒定律，得

2mv1＝3mv2，　②

联立①、②式得

v2＝（1／3）v0．　③

此问也可直接用动量守恒一次求出（从接触到相对静止）mv0＝3mv2，v2＝（1／3）v0．

（2）设弹簧长度被锁定后，贮存在弹簧中的势能为Ep，由能量守恒定律，得

（2m）v12＝（3m）v22＋EP，　④

撞击P后，A与D的动能都为零，解除锁定后，当弹簧刚恢复到自然长度时，弹性势能全部转变成D的动能，设D的速度为v3，有

Ep＝（2m）v32，　⑤

以后弹簧伸长，A球离开挡板P，并获得速度．设此时的速度为v4，由动量守恒定律，得

2mv3＝3mv4，　⑥

当弹簧伸到最长时，其弹性势能最大，设此势能为Ep′，由能量守恒定律，得

（2m）v32＝（3m）v42＋Ep′，　⑦

联立③～⑦式得

Ep′＝mv02．　⑧

点评；　这道高考压轴题不愧为一道好的物理试题．命题人暗设机关，巧布干扰，只有同学们全面读懂、领会题意，并在头脑中建立起非常清晰的物理图景和过程，充分运用两个守恒定律，才能化难为易，正确解题．

例5 。 如图5所示，在倾角为的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k,C为一固定挡板。系统处于静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d，重力加速度为g。

解析：令x1表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知

①

令x2表示B刚要离开C时弹簧的伸长量， a表示此时A的加速度，由胡克定律和牛顿定律可知：

kx2=mBgsinθ ②

F－mA?gsinθ－kx2=mAa ③

由②③式可得 ④

由题意 d=x1+x2 ⑤

由①②⑤式可得 ⑥

例6.如图6所示，劲度系数为k的轻质弹簧一端固定在墙上，另一端和质量为M的容器连接，容器放在光滑水平的地面上，当容器位于O点时弹簧为自然长度，在O点正上方有一滴管，容器每通过O点一次，就有质量为m的一个液滴落入 容器，开始时弹簧压缩，然后撒去外力使容器围绕O点往复运动，求：

(1)容器中落入n个液滴到落入（n+1）个液滴的时间间隔；

(2)容器中落入n个液滴后，容器偏离O点的最大位移。

解析：本题中求容器内落入n个液滴后偏离O点的最大位移时，若从动量守恒和能量守恒的角度求解，将涉及弹簧弹性势能的定量计算，超出了中学大纲的要求，如果改用动量定理和动量守恒定律求解，则可转换成大纲要求内的知识的试题。

(1)弹簧振子在做简谐运动过程中，影响其振动周期的因素有振子的质量和恢复系数(对弹簧振子即为弹簧的劲度系数)，本题中恢复系数始终不变，液滴的落入使振子的质量改变，导致其做简谐运动的周期发生变化。

容器中落入n个液滴后振子的质量为（M+nm），以n个液滴落入后到第（n+1）个液滴落入前，这段时间内系统做简谐运动的周期Tn=2π ，容器落入n个液滴到（n+1）个液滴的时间间隔△t=Tn /2，所以

△t =π

(2)将容器从初始位置释放后，振子运动的动量不断变化，动量变化的原因是水平方向上弹簧弹力的冲量引起的，将容器从静止释放至位置O的过程中，容器的动量从零增至p，因容器位于O点时弹簧为自然长度，液滴在O点处落入容器时，容器和落入的液滴系统在水平方向的合力为零，根据动量守恒定律，液滴在O处的落入并不改变系统水平方向的动量，所以振子处从位置O到两侧相应的最大位移处，或从两侧相应在的最大位移处到位置O的各1/4周期内，虽然周期Tn和对应的最大位移Ln在不断变化，但动量变化的大小均为

△p=p－0=p，

根据动量定理可知，各1/4周期内弹力的冲量大小均相等，即：

F0(t)·T0/4 = Fn(t)·Tn/4

其中T0是从开始释放到第一次到O点的周期，T0=2π 。Tn是n个液滴落入后到（n+1）个液滴落入容器前振子的周期，Tn=2π 。而F0(t) 和Fn(t)分别为第一个1/4周期内和n个液滴落入后的1/4周期内弹力对时间的平均值，由于在各个1/4周期内振子均做简谐运动，因而弹力随时间均按正弦（或余弦）规律变化，随时间按正弦（或余弦）变化的量在1/4周期内对时间的平均值与最大值之间的关系，可用等效方法求出，矩形线圈在匀强磁场中匀速转动时，从中性而开始计地，产生的感应电动势为ε=εmsinωt=　NbωSsinωt。ε按正弦规律变化，根据法拉第电磁感应定律ε=N ，ε在1/4周期内对时间的平均值ε=2εm/π。这一结论对其它正弦（或余弦）变化的量对时间的平均值同样适用，则有图19-1

F0(t)=2kL0/π，Fn(t)=2kLn/π

代入前式解得：Ln= L0

例7．如图7所示，质量为M=3kg的木板静止在光滑水平面上，板的右端放一质量为m=1kg的小铁块，现给铁块一个水平向左速度V0=4m/s，铁块在木板上滑行，与固定在木板左端的水平轻弹簧相碰后又返回，且恰好停在木板右端，求铁块与弹簧相碰过程中，弹性势能的最大值EP。

解析：在铁块运动的整个过程中，系统的动量守恒，因此弹簧压缩最大时和铁块停在木板右端时系统的共同速度（铁块与木板的速度相同）可用动量守恒定律求出。在铁块相对于木板往返运动过程中，系统总机械能损失等于摩擦力和相对运动距离的乘积，可利用能量关系分别对两过程列方程解出结果。

设弹簧压缩量最大时和铁块停在木板右端时系统速度分别为V和V'，由动量守恒得：mV0=(M+m)V=(M+m)V' 所以，V=V’=mV0/(M+m)=1*4/(3+1)=1m/s

铁块刚在木板上运动时系统总动能为：Ek=mV02=8J

弹簧压缩量最大时和铁块最后停在木板右端时，系统总动能都为：

EK'=(M+m)V2=2J

铁块在相对于木板往返运过程中，克服摩擦力f所做的功为：

Wf=f2L=EK-EK'=8-2=6J

铁块由开始运动到弹簧压缩量最大的过程中，系统机械能损失为：fs=3J

由能量关系得出弹性势能最大值为：EP=EK-EK'-fs=8-2-3=3J

点评：由于木板在水平光滑平面上运动，整个系统动量守恒，题中所求的是弹簧的最大弹性势能，解题时必须要用到能量关系。在解本题时要注意两个方面：1.是要知道只有当铁块和木板相对静止时(即速度相同时)，弹簧的弹性势能才最大；弹性势能量大时，铁块和木板的速度都不为零；铁块停在木板右端时，系统速度也不为零。

2.是系统机械能损失并不等于铁块克服摩擦力所做的功，而等于铁块克服摩擦力所做的功和摩擦力对木板所做功的差值，故在计算中用摩擦力乘上铁块在木板上相对滑动的距离。

例8．如图9所示，一劲度系数为k=800N/m的轻弹簧两端各焊接着两个质量均为m=12kg的物体A、B。物体A、B和轻弹簧竖立静止在水平地面上，现要加一竖直向上的力F在上面物体A上，使物体A开始向上做匀加速运动，经0.4s物体B刚要离开地面，设整个过程中弹簧都处于弹性限度内，取g=10m/s2 ，求：

（1）此过程中所加外力F的最大值和最小值。

（2）此过程中外力F所做的功。

解析：(1)A原来静止时：kx1=mg ①

当物体A开始做匀加速运动时，拉力F最小，设为F1，对物体A有：

F1＋kx1－mg=ma ②

当物体B刚要离开地面时，拉力F最大，设为F2，对物体A有：

F2－kx2－mg=ma ③

对物体B有：kx2=mg ④

对物体A有：x1＋x2＝ ⑤

由①、④两式解得 a=3.75m/s2 ，分别由②、③得F1＝45N，F2＝285N

(2)在力F作用的0.4s内，初末状态的弹性势能相等，由功能关系得：

WF=mg(x1＋x2)+49.5J

由以上分析可以看出，弹簧类试题的确能培养我们的物理思维和开发我们的学习潜能。弹簧与相连物体构成的系统所表现出来的运动状态变化的问题，同学们可以充分运用物理概念和规律（牛顿第二定律、动能定理、机械能守恒定律、动量定理、动量守恒定律）巧妙解决。这类题型是区分学生能力强弱、拉大分值差距、选拔人才的一种常规题型。因此，弹簧类试题也就成为高考物理中一种重要的独具特色的题型