浙江高考数学试卷答案,浙江高考数学试卷2021答案

1.想知道2011年数学高考试题和答案(浙江卷）

2.2010年浙江省高考试题：理科数学试卷填空题16题怎么解啊

3.2012浙江高考文科数学选择填空答案？

4.2011年浙江理科高考数学第21题

5.跪求名校导航2019浙江数学高考信息模拟卷答案！有赏！

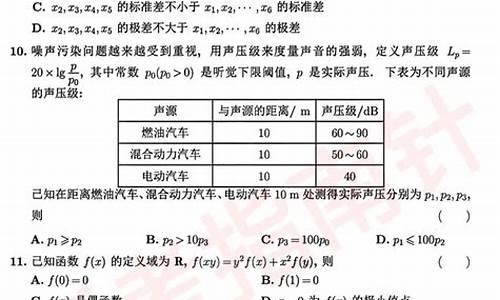
7．（5分）存在函数f（x）满足，对任意x∈R都有（ ）

A． f（sin2x）=sinx B． f（sin2x）=x2+x C． f（x2+1）=|x+1| D． f（x2+2x）=|x+1|

+2x）=|x+1|

试题的意思是，你能不能找到一个函数，满足上面的四个条件之一。

答案是D.

考点： 函数解析式的求解及常用方法．

专题： 函数的性质及应用．

分析： 利用x取特殊值，通过函数的定义判断正误即可．

解答：

解：

A．取x=0，则sin2x=0，∴f（0）=0；

取x=π/2，则sin2x=0，∴f（0）=1；

∴f（0）=0，和1，不符合函数的定义；

∴不存在函数f（x），对任意x∈R都有f（sin2x）=sinx；

B．取x=0，则f（0）=0；

取x=π，则f（0）=π2+π； ∴f（0）有两个值，不符合函数的定义； ∴该选项错误；

C．取x=1，则f（2）=2，取x=﹣1，则f（2）=0； 这样f（2）有两个值，不符合函数的定义； ∴该选项错误；

D．令|x+1|=t，t≥0，则f（t2﹣1）=t；

令t2﹣1=x，则t=√x+1；

∴f(x)=； =√x+1

即存在函数f（x）==√x+1，对任意x∈R，都有f（x2+2x）=|x+1|； ∴该选项正确．

故选：D．

点评： 本题考查函数的定义的应用，基本知识的考查，但是思考问题解决问题的方法比较难．

想知道2011年数学高考试题和答案(浙江卷）

本文将为大家带来，2022浙江高考各科试卷及答案汇总。包括2022年浙江卷英语试卷及答案、2022年浙江卷语文试卷及答案、2022年浙江数学试卷及答案、2022年浙江卷物理试卷及答案、2022年浙江卷历史试卷及答案、2022年浙江卷化学试卷及答案、2022年浙江卷地理试卷及答案。

注：浙江是自主命题省份，因此高考试卷也被称为浙江卷。

一、2022年高考浙江卷语文答案

二、2022年高考浙江卷数学试卷及答案

三、2022年高考浙江卷英语试卷及答案

待更新

四、2022年高考浙江卷物理试卷及答案

五、2022年高考浙江卷历史试卷及答案

六、2022年高考浙江卷化学试卷及答案

七、2022年高考浙江卷生物试卷及答案

八、2022年高考浙江卷地理试卷及答案

九、2022年高考浙江卷政治试卷及答案

2010年浙江省高考试题：理科数学试卷填空题16题怎么解啊

2011年普通高等学校招生全国统一考试（浙江卷）

理科数学

一、选择题

（1）设函数

,则实数

=

（A）-4或-2

（B）-4或2

（C）-2或4

（D）-2或2

（2）把复数

的共轭复数记作

，i为虚数单位，若

（A）3-i

（B）3+i

（C）1+3i

（D）3

（3）若某集合体的三视图如图所示，则这个集合体的直观图可以是

(4)下列命题中错误的是

（A）如果平面

，那么平面

内一定存在直线平行于平面

（B）如果平面

不垂直于平面

，那么平面

内一定不存在直线垂直于平面

（C）如果平面

，平面

，那么

（D）如果平面

，那么平面

内所有直线都垂直于平面

（5）设实数

满足不等式组

若

为整数，则

的最小值是

（A）14

（B）16

（C）17

（D）19

（6）若

，则

（A）

（B）

（C）

（D）

（7）若

为实数，则“

”是

的

（A）充分而不必要条件

（B）必要而不充分条件

（C）充分必要条件

（D）既不充分也不必要条件

（8）已知椭圆

与双曲线

有公共的焦点，

的一条渐近线与以

的长轴为直径的圆相交于

两点，

若

恰好将线段

三等分，则

（A）

（B）

（C）

（D）

（9）有5本不同的书，其中语文书2本，数学书2本，物理书1本.若将其随机的并排摆放到书架的同一层上，则同一科目的书都不相邻的概率

（A）

（B）

（C）

D

（10）设a，b，c为实数，f（x）

=（x+a）

.记集合S=

若

分别为集合元素S，T的元素个数，则下列结论不可能的是

（A）

=1且

=0

（B）

（C）

=2且

=2

（D）

=2且

=3

非选择题部分

（共100分）

二、填空题：本大题共7小题，每小题4分，共28分

（11）若函数

为偶函数，则实数

=

（12）若某程序图如图所

示，则该程序运行后输出的k的值是

（13）设二项式（x-

）n(a>0)的展开式中X的系数为A,常数项为B，

若B=4A，则a的值是

（14）若平面向量α，β满足|α|≤1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为

，则α与β的夹角

的取值范围是

（15）某毕业生参加人才招聘会，分别向甲、乙、丙三个公

司投递了个人简历，假定该毕业生得到甲公司面试的概率为

，得到乙公司面试的概率为

，且三个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若

，则随机变量X的数学期望

（16）设

为实数，若

则

的最大值是

.。

（17）设

分别为椭圆

的焦点，点

在椭圆上，若

;则点

的坐标是

.

三、解答题;本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤。

（18）（本题满分14分）在

中，角

所对的边分别为a,b,c.

已知

且

.

（Ⅰ）当

时，求

的值；

(Ⅱ)若角

为锐角，求p的取值范围；

（19）（本题满分14分）已知公差不为0的等差数列

的首项

为a(

),设数列的前n项和为

，且

成等比数列

（1）求数列

的通项公式及

（2）记

，当

时，试比较

与

的大小.

（20）（本题满分15分）如图，在三棱锥

中，

，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2

（Ⅰ）证明：AP⊥BC；

（Ⅱ）在线段AP上是否存在点M，使得二面角A-MC-β为直二面

角？若存在，求出AM的长；若不存在，请说明理由。

（21）（本题满分15分）已知抛物线

:

＝

，圆

:

的圆心为点M

（Ⅰ）求点M到抛物线

的准

线的距离；

（Ⅱ）已知点P是抛物线

上一点（异于原点），过点P作圆

的两条切线，交抛物线

于A，B两点，若过M，P两点的直线

垂直于

AB，求直线

的方程

（22）（本题满分14分）

设函数

（I）若

的极值点，求实数

（II）求实数

的取值范围，使得对任意的

，恒有

成立，注：

为自然对数的底数。

2012浙江高考文科数学选择填空答案？

首先以单位长度1也就是向量b的模为半径画圆。从圆心引出一条射线。在这条射线上找到一点引出的射线与从圆心引出的这条夹角是60度，与园相切。从圆心到这个点的距离是最大值。a的范围就是0到这个值。可以求出a

max=2倍根号3

/3。

下面解释原因。首先向量b-a就是从a的端点指向b的端点的向量，他与a的夹角是120度，所以a的要取60度角（也就是这两条向量是夹120度角）。

所以所有的和从原点引出的直线呈60度夹角的射线中能和圆有交点的都可以取到。不包括圆心（题目中说的a不等于0）。

所以最外面的可以到与园相切的这条，之后的都不行了。所以算出a的范围是（0，2倍根号3

/3]

2011年浙江理科高考数学第21题

1-5.DDACB 6-10. ACBCA

11.160 12.2/5 13.1/120 14. [0,7/2] 15.-16 16.3/2 17. 9/4

跪求名校导航2019浙江数学高考信息模拟卷答案！有赏！

（21）（21）（本题满分15分）已知抛物线＝，圆的圆心为点M。

（Ⅰ）求点M到抛物线的准线的距离；

（Ⅱ）已知点P是抛物线上一点（异于原点），过点P作圆的两条切线，交抛物线于A，B两点，若过M，P两点的直线垂足于AB，求直线的方程.

（Ⅰ）解：由题意可知，抛物线的准线方程为：所以圆心M（0,4）到抛物线的距离是

（Ⅱ）解：设P(x0, x02)，A（）B（），由题意得设过点P的圆C2的切线方程为y-x0=k(x- x0)

即， ①

则

即

设PA，PB的斜率为，则是上述方程的两根，所以

，

将①代入得，

由于是此方程的根，故所以

由MP⊥AB,得，解得

即点P的坐标为，所以直线l的方程为。 (请下载原试题)

2019 年浙江省高考信息模拟卷数学（一 ）

试卷分第 I 卷（选择题）和第 II 卷（非选择题）两部分，全卷满分 150 分，考试时间 120 分钟. 第 I 卷（选择题 共 40 分）

一、选择题（本大题共 10 小题，每小题 4 分共 40 分，在每小题给出的四个选项中，只有一项

是符合题目要求的. ）

1. 已知集合 2 x ，则 （ ） M {x |y x ? 4x ? 5}, N {y | y ln(e +1)} (C M ) N R A. (1,5) B. (0,5) C. (1,5] D. (0,5] | z1 |

2. 若z1 3=?i, z 2 1=+3i ，则 （ ） | z2 | A. 1 B. 2 C. 3 D. 10 | a |?b

3. 已知a,b ?R ，则“ ”是a ?|b |的 （ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件

4. 设函数 ，则 的奇偶性 （ ） f (x ) sin(?x =+?)( 0) f (x ) A.与 有关，且与 有关 B.与 有关，但与 无关 C.与 无关，且与 无关 D.与 无关，但与 有关 V ,V V ?V

5. 两个几何体的三视图如图所示，记几何体的体积为 1 2 ，则 2 1 （ ） 2 2 A. B. C. D. 3 6 3 6 ? x ? 3y ? 0

6. 已知 ，点 ，则 S {(x , y ) |?x =+ 3y ? 6 3 ? 0} P( 3,3), T {N | PM =+PN 0,M =?S} ? x ? 0 S T 的面积为 （ ） A. 3 3 B. 6 C. 6 3 D. 9

7. 如图，已知正四棱锥P ?ABCD 的各棱长均相等 ，M 是 上的动点（不包括端点）， 是 的中点，分别记 AB N AD 二面角P ?MN ?C ,P ?AB ?C ,P ?MD ?C 为?,?,? ， 则 （ ） A. ? B. ? C. ? D. ?

8. 对函数f (x ) x 2 =+a ln(x 4 +x 2 +1)(x ?R ) 的极值和最值情况，一定 （ ） A.既有极大值，也有最大值 B.无极大值，但有最大值 C.既有极小值，也有最小值 D.无极小值，但有最小值 2 2 x y F E : + 1(a =?b ? 0)

9. 如图，点 为椭圆 2 2 的右焦点 ， a b 2 2 2 M y 点 时圆O : x + y b 上一动点（ 轴右侧） ，过 M 作圆 的切线交椭圆于A,B 两点，若?ABF 的周长 O 为3b ，则椭圆 的离心率为 （ ） E 2 2 5 3 A. B. C. D. 3 2 3 2 R f (?x ) +f (x ) x 2 x ? 0

10.定义在 上的可导函数f (x ) 满足 ，当 时，f '(x ) ?x ，则不等式 1 3 2 f (x +1) ?f (2x ) ? +x ? x 的解集为 （ ） 2 2 A. [1,+?) B. (?,1] C. (?,2] D. [2,+?) 第 II 卷（非选择题 共 110 分）

二、填空题（本大题共 7 小题，多空题每小题 6 分，单空题每小题 4 分，共 36 分. ）

11.集合 ， ，则 ， U {x |1=? x ? 9, x? N} A {1,3,5,7}, B {5,6,7,8,9} A B (C A) (C B) . U U ? 3 ? 2

12.若sin( ) , ?=? (0, ) ，则sin? ，sin2? +cos ? . 4 5 2

13.双曲线E : 4x2 ? y 2 1 ，则渐近线方程为 ，以焦点为圆心，与渐近线相切得 圆的面积为 .

14.已知x2 +x8 a =+a (2 +x ) +a (2 +x )2 + +a (2 +x )8 ，则a ， 0 1 2 8 7 a +a +a + +a +a . 0 1 2 7 8

15.甲乙两袋中各有4 个大小相同，形状一样，质地均匀的小球，其中甲袋中3 红1 白，乙袋中 3 白1 红，现同时从甲乙两袋中各摸出2 个球交换，则交换后甲袋中红球的个数 的数学期 ? 望E (?) .

16.已知 满足| a | 2,(a =+b)?b 8 ，则 的取值范围为 . a,b a ?b a

17.设函数f (x ) 1=?x + 4 ?x ，g (x ) (a =?R ) ，若对任意的x ?(0,1) ，恒有f (x ) ? x a g (x ) 成立，则实数 的取值范围是 多少？

全部题请看如下：